2017 : msjmeeting-2017sep-11i002 Ding-Iohara-Miki ( ) 1. Ding-Iohara-Miki - - [1, 2] [3, 4] gl(1) [5] 2 2 q- [6] q-w N [7, 8] [9] [10] W 1
|
|
|
- Trương Kim
- 4 năm trước
- Lượt xem:
Bản ghi
1 2017 : msjmeeting-2017sep-11i002 Ding-Iohara-Miki 1. Ding-Iohara-Miki - - [1, 2] [3, 4] gl1 [5] 2 2 q- [6] q-w N [7, 8] [9] [10] W [1, 2] [3, 4] z C D := z d dz z Dk z n = z n D + n k W 1+ 1 z n D k n Z, k Z 0 W W z n D k n Z, k Z 0 [W z n D k, W z m D l ] = W [z n D k, z m D l ] n ψn,m k,l j=1 jk n j l, n > 0, = 0, n = 0, m j=1 jl n j k, n < 0 + cψ k,l n,mδ n+m,0, 1 c C q- q C D k q D z q D z = qzq D D q D z W 1+ W z n q kd [W z n q kd, W z m q ld ] = q mk q nl W z n+m q k+ld q mk q nl + cδ n+m,0 3 1 q k+l : ,17K Mathematics Sbject Classification: 81R10,81T13,33D45,AGT,, awata@math.nagoya-.ac.jp web: W 2
2 k + l 0 3 k 0 W q kd W q kd new = W q kd + c 1 q k k + l = 0 ncq nk δ n+m,0 δ k+l,0 k + l = 0 k = l = 0 z q D n k W 1+ k < 0 2 W : W 2 1+ := W z n q kd n,k Z. [W z n q kd, W z m q ld ] = q mk q nl W z n+m q k+ld + q nk nc 1 + kc 2 δ m+n,0 δ k+l,0 4 2 c 1, c 2 C 2.3. t- - - N z = z 1, z 2,, z N D i := z i z i N z i q D i z j = q δ i,j z j q D i W z iq kd i N t C N x ± tz i z j n := W q ±1 z i n q ±D i 5 z i z j j [2] - - x + 0 k = ±1 k = ±1 W 2 1+ z i q D i z q D [2] z C x ± z = n Z x± n z n, ψ ± z = ±n N ψ± n z n q, t C F = Qq, t F = Qq 1/4, t 1/4 G ± z := 1 q ±1 z1 t 1 z1 q/t 1 z = z 3 G z 1, 6 gz := G+ z G z = g 1 z 1 Qq, t[[z]] 7 z < 1 G ± z = exp z n n q±n + t n + q/t n, 8 n>0 z n gz = exp n 1 qn 1 t n 1 q/t n. 9 n>0
3 - - U gγ 1 w/z gγ +1 w/z ψ+ zψ w = ψ wψ + z, [ψ ± z, ψ ± w] = 0, 10 gγ 1/2 w/z ±1 ψ + zx ± w = x ± wψ + z, 11 ψ zx ± w = x ± wψ zgγ 1/2 z/w ±1, 12 G ± w/zx ± zx ± w = x ± wx ± z w 3 G ± z/w, 13 z [x + z, x 1 q1 1/t w] = δγ 1 z/wψ + γ 1/2 w δγz/wψ γ 1/2 w 1 q/t 14 F δz = n Z zn γ ±1/2 ψ 0 ± M F U- α M γ 1/2 α = t/q l 1/4 α, ψ ψ 0 α = t/q l 2 α 15 M l 1, l 2 U [1] γ ±1/2 = γ ±1/2 γ ±1/2, 16 x + z = x + z 1 + ψ γ 1/2 1 z x+ γ 1 z, 17 x z = x γ 2 z ψ + γ 1/2 2 z + 1 x z, 18 ψ ± z = ψ ± γ ±1/2 2 z ψ ± γ 1/2 1 z 19 γ ±1/2 1 = γ ±1/2 1 γ ±1/2 2 = 1 γ ±1/2 3. Boson W Boson 3.1. Boson [a m, a n ] = m 1 q m 1 t m δ m+n,0 a 0 20 a n n Z F H 0 a n 0 = 0 n Z >0 λ = λ 1, λ 2,..., λ 1 λ a λ = a λ1 a λ2 0 a λ F 0 0 a n = 0 n Z <0 a λ = 0 a λ1 a λ2 a λ F , N F 1,N 0, 0 x + 0
4 [8] 1, 0 k = ±1 l 2 x + z x w δ δγ ±1 z/w γ ±1 l 2 x + z := exp x z := exp ψ ± z := exp 1 t n a n z n exp n 1 t n t/q n/2 a n z n exp n 1 t n n a nz n z N q/t N/2, 21 1 t n n t/qn/2 a n z n 1 z N q/t N/2, 22 1 t ±n 1 t/q n q/t n/4 a ±n z q/t n ±N/2 23 n C N Z F F U- [11, 10] γ 1/2 = t/q 1/4 1, N F 1,N 0, 1 [12, 13] 3.3. q-w N - - l 1 l 2 2 N q-w N q-w 2 = q- N N 2 N, 0 1, 0 N N i x +i z, ψ i z q-w N T i z := 1 j 1 < <j i N Λ j 1 zq/t 1 i 2 Λ j 2 zq/t 3 i 2 Λ j i zq/t i 1 2, 24 Λ i z := ψ 1 zψ 2 zq/t 1 2 ψ i 1 zq/t 2 i 2 x +i zq/t 1 i 2 25 q-w N T N z id - - q-w N q-w N T N z N N 1 q-w N q-w N 3.4. λ = λ 1, λ 2,... λ 1 λ 2 λ := λ i < λ λ lλ := λ 1, := 0, 0, i, j λ {i, j Z 2 1 i lλ, 1 j λ i }
5 F 1,0 0 x + z x + 0 x + 0 P λ = ε λ P λ, ε λ = 1 + t 1 l q λ i 1t i, 26 P λ = P λ a 1, a 2, 0 F 1, p = p 1, p 2,, p n C 1 t n a n Cp := exp 1 q n n p n n>0 28 n > 0 p n 0 Cp = 0 Cp a n, 29 n 1 qn 1 t n p n 0 Cp = 0 Cp a n 30 0 Cp a n, a n n N p p n, p n n N P λ/µ p P µ Cp P λ 31 P λ/µ p p n := xn i [14] 4. [10] 4.1. Φ 2 F l 1,l 2 F r 1,r 2 v F l 1+r 1,l 2 +r 2 +v l 1, l 2 = 1, N 0, 1 N Z,,, w C 3 Φ Φ : F z 0,1 F 1,N 1 F 1,N z, λ, 32 XΦ = Φ X X U, N N 1 33 F 0,1 P λ Φ Φ λ z Φ λ zα = ΦP λ α P λ α F 0,1 z X F 0,1 ad X, 33 F 1,N 1 34 ad ψ ± z, Φ λ w := ψ ± q/t ±1/4 zφ λ w ψ + q/t ±1/4 z 1, 35 ad x + z, Φ λ w := x + zφ λ w ad ψ z, Φ λ w x + z, 36 ad x z, Φ λ w := [ x q/t 1/2 z, Φ λ w ] ψ + q/t 1/4 z 1 37
6 Φ λ w 3637 δ δ w/z z, w Φ λ w ad x z, λ = Φ w δ = /z ad x + z, Φ λ w Φ λ w ad X, 0, 1 [ z, λ ] Φ λ z = Φ /z = P λ t ρ 1 2 x + q j 1 t 1 i z Φ z, 38 N N 1 Φ z = exp i,j λ 1 1 n 1 q a nz n 1 q n exp n n 1 q a nz n. 39 n x +, N F 1,N P λ t ρ 1 2 c C p n cq λ t ρ := c n q nλ i 1t n 1 2 i c n + 40 t n 2 t n 2 λ =, c = t 1 2 P λ ct ρ 1 2 := Pλ ct ρ 1 2 ; q, t = i,j λ cq j 1 1 q λ i j t λ i+1 x + q j 1 t 1 i z Φ z = q j t 2 i z N i,j λ i,j λ 1 1 t n exp n 1 q a nq/t n/2 z/q 1 n 2 n p n q λ t ρ 1 1 t n exp n 1 q a nq/t n/2 z/q 1 n 2 n p n q λ t ρ 28 C p C p p := p 1, p 2,, p := p 1, p 2, , 1 F 0,1 w 38 ad X, 0, 1 F w 0,1 [12, 13] ad ψ ± z, Φ λ w = q/t ±1/2 B ± λ w/z±1 Φ λ w, 43 ad x + z, Φ λ w = lλ+1 A + λ,i δqλ i t 1 i w/zφ λ+1i w, 44 ad x z, Φ λ w lλ = q/t 1/2 A λ,i δqλ i 1 t 1 i w/zφ λ 1i w 45
7 := q λ i t i i 1 A + λ,i := 1 t 1 t x j 1 q t x j, 46 j=1 1 x j 1 q x j 1 t x j A λ,i := 1 1 q x j t t 1 j=i+1 1 x j 1 q x j = 1 t 1 1 t x l+1 l 1 t x j 1 q x j t 1 q x, 47 l+1 j=i+1 1 x j 1 q x j B ± λ z := 1 zx ±1 1 z t2 q i ±1 1 zt ±1 1 z t x 48 q i ±1 λ i = λ i 1 A + λ,i = 0, λ i = λ i+1 A λ,i = 0 λ i < λ i 1, i- λ + 1 i = λ 1, λ 2,..., λ i 1, λ i + 1, λ i+1,... λ i > λ i+1, i- λ 1 i = λ 1, λ 2,..., λ i 1, λ i 1, λ i+1, Φ Φ Φ λ Φ : F 1,N+1 F 1,N F z 0,1, N N+1 49 XΦ = Φ X X U z, λ 50 Φ α = λ Φ λzα P λ / P λ P λ α F 1,N+1 51 P λ P λ P λ P λ := P λ, P λ q,t = 1 q λi j+1 t λ i 1 q λ i j t λ i+1 i,j λ 52 X F 0,1 ad X, 50 ad ψ ± z, Φ λw := ψ ± q/t 1/4 z 1 Φ λ wψ ± q/t 1/4 z, 53 ad x + z, Φ λw := ψ q/t 1/4 z 1 [ x + q/t 1/2 z, Φ λw ], 54 ad x z, Φ λw := x zad ψ + z, Φ λw Φ λwx z 55
8 x + z λ = Φ w = z [ ] z Φ λz = Φ N N+1 = P λ qt ρ 1 2 x q j 1 t 1 i z Φ z, 56 z, λ i,j λ Φ 1 1 z = exp n 1 q n t/qn/2 a n z n 1 q n exp n 1 q n t/qn/2 a n z n 57 x, N F 1,N i,j λ exp x q j 1 t 1 i z Φ z = i,j λ q j 1 2 t 1 2 i z N t n n 1 q a nz/q 1 n 2 n p n q λ t ρ 1 1 t n exp n 1 q a nz/q 1 n 2 n p n q λ t ρ 28 Cp C p ad X, 4.4. ad ψ ± z, Φ λw = q/t ±1/2 B ± λ w/z±1 Φ λ, 59 ad x + z, Φ λw lλ = q A λ,i δqλ i 1 t 1 i w/zφ λ 1 i w, 60 ad x z, Φ λw lλ+1 = q/t 1/2 q 1 A + λ,i δqλ i t 1 i w/zφ λ+1 i w 61 F 0,1 [ w, µ z, λ ] [ w, µ ] [ z, λ ] Φ zw z N+2 N+1 N := Φ zw z N+2 N+1 Φ z = Φ λ wφ λ z 62 2 F 1,N [ ] v/z v v/z v M 1 M Φ z z := λ Φ 1 P λ P λ [ Φ M 1 z, λ z, λ M z λ ] = λ 1 P λ P λ Φ λ z Φ λ z 63
9 4.5. v/z v M 1 M Φ z z { Sx := exp 1 1 t n 1 + n 1 q n n 1 α n = i 1 Sq λ i t ρ i q 1/2 z, 64 } { q n x n α n exp t n t n 1 + n 1 q n q t n x n α n }, 65 1 a1 1 + q/t n n q/t n /2 a 2 n 66 a 1 n = a n 1 a 2 n = 1 a n Sz q- - - X U v/z v M 1 M X, Φ z = 0 67 z [15] 5. AGT 5.1. ι ιp n = p n, ιa n = a n n > 0 [10] [ z, λ ] ιp µ Φ z ιp ν C µλ νq, t, 68 [ ] z ιp ν Φ N N+1 ιp µ C ν µλ q, t 69 z, λ C µλ ν q, t = P λ t ρ ; q, t σ ιp µ /σ tλ q ρ ; t, qp ν/σ q λ t ρ ; q, tq 1/2 /t 1/2 σ ν f ν q, t 1, C µλ νq, t = 1 λ + µ + ν C µ λ ν t, q 71 [16] f λ q, t := i,j λ 1qj 1 2 t 1 2 i 28 Cp, C p 31 Iqbal-Kozcaz-Vafa [17] [18] 70
10 SU2 N f = 0 v/z 0 1 z 2 v/z 1 v M 2 M 1 M 0 Φ z 2 z z 1 z 2 z 1 0 N+2 2 N f 0 SUN, N > 2 q- q-w N AGT [19][20] U1 [21] - - [10] qt-kz [22] [1] J. Ding, K. Iohara, Lett. Math. Phys , no. 2, [2] K. Miki, J. Math. Phys [3] V. Kac and A. Radl, Comm. Math. Phys [4] H. Awata, M. Fkma, Y. Matso and S. Odake, Prog.Theor.Phys.Sppl [5] V. Ginzbrg, M. Kapranov and E. Vasserot, Mathem. Research Letters, [6] J. Shiraishi, H. Kbo, H. Awata, S. Odake, Lett. Math. Phys , [7] B. Feigin and E. Frenkel, Comm. Math. Phys [8] H. Awata, H. Kbo, S. Odake and J. Shiraishi, Comm. Math. Phys [9] N. Nekrasov, Adv. Theor. Math. Phys [10] H. Awata, B. Feigin and J. Shiraishi, JHEP [11] B. Feigin, K. Hashizme, A. Hoshino, J. Shiraishi, S. Yanagida, J. Math. Phys [12] B. Feigin, A. Tsymbalik, Kyoto J. Math [13] B. Feigin, E. Feigin, M. Jimbo, T. Miwa, E. Mkhin, Kyoto J. Math [14] H. Awata, S. Odake and J. Shiraishi, Comm. Math. Phys. 179, [15] H. Awata, H. Kanno, T. Matsmoto, A. Mironov, A. Morozov, An. Morozov, Y. Ohkbo and Y. Zenkevich, JHEP [16] H. Awata, H. Kanno, JHEP 0505, ; Int. J. Mod. Phys. A [17] A. Iqbal, C. Kozcaz and C. Vafa, J. High Energy Phys no. 10, 069, 58pp. [18] H. Awata, 2009,, [19] L.F. Alday, D. Gaiotto, Y. Tachikawa, Lett. Math. Phys , [20] H. Awata, Y. Yamada, JHEP 1001: ; Prog. Theor. Phys , [21] V.A. Alba, V.A. Fateev, A.V. Litvinov, G.M. Tarnopolsky, Lett. Math. Phys [22] H. Awata, H. Kanno, A. Mironov, A. Morozov, An. Morozov, Y. Ohkbo and Y. Zenkevich, Jor. High Energy Phys ; Ncl. Phys. B ; Phys. Rev. D
Đề chọn đội VMO 2016 Người tổng hợp: Nguyễn Trung Tuân Ngày 16 tháng 12 năm 2015 Tóm tắt nội dung Tài liệu chứa các đề chọn đội VMO 2016 của các tỉnh.
 Đề chọn đội VMO 2016 Người tổng hợp: Nguyễn Trung Tuân Ngày 16 tháng 12 năm 2015 Tóm tắt nội dung Tài liệu chứa các đề chọn đội VMO 2016 của các tỉnh. Mục lục 1 Hà Nội 4 2 Thành phố Hồ Chí Minh 5 2.1 Ngày
Đề chọn đội VMO 2016 Người tổng hợp: Nguyễn Trung Tuân Ngày 16 tháng 12 năm 2015 Tóm tắt nội dung Tài liệu chứa các đề chọn đội VMO 2016 của các tỉnh. Mục lục 1 Hà Nội 4 2 Thành phố Hồ Chí Minh 5 2.1 Ngày
01_Phep tinh tien_Baigiang
 Tài liệ bài giảng (Toán 11 Moon.n) 01. PHÉP TỊNH TIẾN Thầy Đặng Việt Hùng VIDEO ÀI GIẢNG à LỜI GIẢI CHI TIẾT CÁC ÀI TẬP chỉ có tại website MOON.VN Lí thyết cơ bản: Xét phép tịnh tiến theo éc tơ, khi đó
Tài liệ bài giảng (Toán 11 Moon.n) 01. PHÉP TỊNH TIẾN Thầy Đặng Việt Hùng VIDEO ÀI GIẢNG à LỜI GIẢI CHI TIẾT CÁC ÀI TẬP chỉ có tại website MOON.VN Lí thyết cơ bản: Xét phép tịnh tiến theo éc tơ, khi đó
Founder PS conv standard PS By [
 6 &.9 & 39&58 &8;&(9) +$6 +$ %! $ $ ' ' $ ']^ $ %&' (P23$'Q_:; C?=:; 78Q_:;(_` KUP23- 'Q:;+ /@,?=/;&QU:; + -% 4526%A,:O&K23 O%K _:; / &' 23&%A@:O' O$K 23$'Q:@ 0C, 2 3-'Q_:;,+`>/ 23-'Q _:;?= K!! " # ( )*+,#
6 &.9 & 39&58 &8;&(9) +$6 +$ %! $ $ ' ' $ ']^ $ %&' (P23$'Q_:; C?=:; 78Q_:;(_` KUP23- 'Q:;+ /@,?=/;&QU:; + -% 4526%A,:O&K23 O%K _:; / &' 23&%A@:O' O$K 23$'Q:@ 0C, 2 3-'Q_:;,+`>/ 23-'Q _:;?= K!! " # ( )*+,#
coursalgebre.dvi
 Ð Ö Ô ØÖ ¾ Ê Ú ÓÒ Å ØÖ ¾º½ ¾º½º½ Ò Ø ÓÒ Ø ÓÔ Ö Ø ÓÒ Ð Ñ ÒØ Ö Ò Ø ÓÒ Ò Ø ÓÒ ¾º½º½ ÍÒ Ñ ØÖ Ø ÐÐ n m n Ð Ò Ø m ÓÐÓÒÒ µ Ó ÒØ Ò K Ø Ð ÓÒÒ ³ÙÒ Ñ ÐÐ A = (a i,j ) 1 i n ³ Ð Ñ ÒØ Kº ij Ò Ñ Ð Ñ ØÖ Ø ÐÐ n m 1 j m
Ð Ö Ô ØÖ ¾ Ê Ú ÓÒ Å ØÖ ¾º½ ¾º½º½ Ò Ø ÓÒ Ø ÓÔ Ö Ø ÓÒ Ð Ñ ÒØ Ö Ò Ø ÓÒ Ò Ø ÓÒ ¾º½º½ ÍÒ Ñ ØÖ Ø ÐÐ n m n Ð Ò Ø m ÓÐÓÒÒ µ Ó ÒØ Ò K Ø Ð ÓÒÒ ³ÙÒ Ñ ÐÐ A = (a i,j ) 1 i n ³ Ð Ñ ÒØ Kº ij Ò Ñ Ð Ñ ØÖ Ø ÐÐ n m 1 j m
CDH
 Fluid Power Technology & Industrial Automation Xilanh thủy lực Tiêu chuẩn ISO 60 Kiểu CDH Star Hydraulics No. 2/20/8 - Thụy Khuê - Q. Tây Hồ - Hà Nội http://www.thuyluc.com Fax ++84-4-6873585 E-mail: starhydraulics@vnws.com
Fluid Power Technology & Industrial Automation Xilanh thủy lực Tiêu chuẩn ISO 60 Kiểu CDH Star Hydraulics No. 2/20/8 - Thụy Khuê - Q. Tây Hồ - Hà Nội http://www.thuyluc.com Fax ++84-4-6873585 E-mail: starhydraulics@vnws.com
TUYỂN TẬP ĐỀ THI HSG TỈNH 9 NĂM Thực hiện bởi NHÓM MATH-TEX Phạm Quốc Sang - Lê Minh Cường Phạm Hữu
 TUYỂN TẬP ĐỀ THI HSG TỈNH 9 NĂM 2017-2018 Thực hiện bởi NHÓM MATH-TEX https://www.facebook.com/groups/mathtex/ Phạm Quốc Sang - Lê Minh Cường Phạm Hữu Hiệp Nguyễn Sỹ Trang Nguyễn Nguyễn Thành Khang Dũng
TUYỂN TẬP ĐỀ THI HSG TỈNH 9 NĂM 2017-2018 Thực hiện bởi NHÓM MATH-TEX https://www.facebook.com/groups/mathtex/ Phạm Quốc Sang - Lê Minh Cường Phạm Hữu Hiệp Nguyễn Sỹ Trang Nguyễn Nguyễn Thành Khang Dũng
examens préopératoires
 !{ > > r O! z 1 UD CN T1l(, > :. (Dll )Ë JX l:1 (,) U, OJ lq) : _. ' )(' ^ X '. $.. tr s*r ËË ru, p (] C" {.l:, { z l t, >!< 8 > ^{!l) v U' V P ) ^ Ër âë (r V A ^È :' â l> '{ ' C] e {l O :'... * ' V À
!{ > > r O! z 1 UD CN T1l(, > :. (Dll )Ë JX l:1 (,) U, OJ lq) : _. ' )(' ^ X '. $.. tr s*r ËË ru, p (] C" {.l:, { z l t, >!< 8 > ^{!l) v U' V P ) ^ Ër âë (r V A ^È :' â l> '{ ' C] e {l O :'... * ' V À
Báo cáo thường niên Doanh nghiệp Việt Nam 2010
 PHÒNG THƯƠNG MẠI VÀ CÔNG NGHIỆP VIỆT NAM BÁO CÁO THƯỜNG NIÊN DOANH NGHIỆP VIỆT NAM 2012 Chủ đề năm : Chặng đường 10 năm phát triển và Năng lực tiếp cận thị trường 18/04/2012 QUY MÔ BÌNH QUÂN CỦA DOANH
PHÒNG THƯƠNG MẠI VÀ CÔNG NGHIỆP VIỆT NAM BÁO CÁO THƯỜNG NIÊN DOANH NGHIỆP VIỆT NAM 2012 Chủ đề năm : Chặng đường 10 năm phát triển và Năng lực tiếp cận thị trường 18/04/2012 QUY MÔ BÌNH QUÂN CỦA DOANH
H20_新人戦(団体登録)
 '678'9:;? -. B CDE CD CDF CDG CDH " & ' ( *, -. / 0 1 2. 3 4 5 6. ' 0 7 8 9 : ; ? 9 B C D E. F G H I. J 0 K L. M N O P Q ' R. T UVW X Y D Z [ 0 \ Q. " 3 H ] ^. _ [ ` a. 9 ' b 8. c d e. f UVg h
'678'9:;? -. B CDE CD CDF CDG CDH " & ' ( *, -. / 0 1 2. 3 4 5 6. ' 0 7 8 9 : ; ? 9 B C D E. F G H I. J 0 K L. M N O P Q ' R. T UVW X Y D Z [ 0 \ Q. " 3 H ] ^. _ [ ` a. 9 ' b 8. c d e. f UVg h
CÁC DẠNG TOÁN 11 CHƯƠNG III. QUAN HỆ VUÔNG GÓC Câu 1. Câu 2. Trong không gian, A. vectơ là một đoạn thẳng. B. vectơ là một đoạn thẳng đã phân biệt điể
 CHƯƠNG III. QUAN HỆ VUÔNG GÓC Câu 1. Câu. Trong không gian, vectơ là một đoạn thẳng. B. vectơ là một đoạn thẳng đã phân biệt điểm nào là điểm đầu, điểm nào là điểm cuối. vectơ là hình gồm hai điểm, trong
CHƯƠNG III. QUAN HỆ VUÔNG GÓC Câu 1. Câu. Trong không gian, vectơ là một đoạn thẳng. B. vectơ là một đoạn thẳng đã phân biệt điểm nào là điểm đầu, điểm nào là điểm cuối. vectơ là hình gồm hai điểm, trong
Ứng dụng của tỉ số phương tích Nguyễn Văn Linh Sinh viên K50 TCNH ĐH Ngoại thương 1 Giới thiệu Chúng ta bắt đầu từ công thức hiệu số phương tích của m
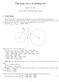 Ứng dụng của tỉ số phương tích Nguyễn Văn Linh Sinh viên K50 TNH ĐH Ngoại thương 1 Giới thiệu húng ta bắt đầu từ công thức hiệu số phương tích của một điểm đối với hai đường tròn ho hai đường tròn không
Ứng dụng của tỉ số phương tích Nguyễn Văn Linh Sinh viên K50 TNH ĐH Ngoại thương 1 Giới thiệu húng ta bắt đầu từ công thức hiệu số phương tích của một điểm đối với hai đường tròn ho hai đường tròn không
HOC360.NET - TÀI LIỆU HỌC TẬP MIỄN PHÍ HAI ĐƯỜNG THẲNG VUÔNG GÓC A. CHUẨN KIẾN THỨC A.TÓM TẮT GIÁO KHOA. 1. Định nghĩa: B. LUYỆN KĨ NĂNG GIẢI CÁC DẠNG
 HI ĐƯỜNG THẲNG VUÔNG GÓ HUẨN KIẾN THỨ TÓM TẮT GIÁO KHO 1 Định nghĩa: LUYỆN KĨ NĂNG GIẢI Á ẠNG ÀI TẬP ài toán 1: TÍNH GÓ GIỮ HI ĐƯỜNG THẲNG Phương pháp: Để tính góc giữa hai đường thẳng d,d trong không
HI ĐƯỜNG THẲNG VUÔNG GÓ HUẨN KIẾN THỨ TÓM TẮT GIÁO KHO 1 Định nghĩa: LUYỆN KĨ NĂNG GIẢI Á ẠNG ÀI TẬP ài toán 1: TÍNH GÓ GIỮ HI ĐƯỜNG THẲNG Phương pháp: Để tính góc giữa hai đường thẳng d,d trong không
ĐẠI HỌC QUỐC GIA HÀ NỘI TRƯỜNG ĐẠI HỌC KHOA HỌC TỰ NHIÊN KHOA TOÁN-CƠ-TIN HỌC NGUYỄN THỊ QUỲNH VỀ PHỨC KOSZUL TÓM TẮT LUẬN VĂN THẠC SĨ Chuyên ngành: Đ
 ĐẠI HỌC QUỐC GIA HÀ NỘI TRƯỜNG ĐẠI HỌC KHOA HỌC TỰ NHIÊN KHOA TOÁN-CƠ-TIN HỌC NGUYỄN THỊ QUỲNH VỀ PHỨC KOSZUL TÓM TẮT LUẬN VĂN THẠC SĨ Chuyên ngành: Đại số và lý thuyết số Giảng viên hướng dẫn: TS. Nguyễn
ĐẠI HỌC QUỐC GIA HÀ NỘI TRƯỜNG ĐẠI HỌC KHOA HỌC TỰ NHIÊN KHOA TOÁN-CƠ-TIN HỌC NGUYỄN THỊ QUỲNH VỀ PHỨC KOSZUL TÓM TẮT LUẬN VĂN THẠC SĨ Chuyên ngành: Đại số và lý thuyết số Giảng viên hướng dẫn: TS. Nguyễn
ĐẠI HỌC CÔNG NGHIỆP THÀNH PHỐ HỒ CHÍ MINH Ths. Ngô Quốc Nhàn BÀI GIẢNG TOÁN CAO CẤP A2 Hệ Đại Học Ngành: Thời lượng giảng dạy: 45 tiết. TP.HỒ CHÍ MINH
 ĐẠI HỌC CÔNG NGHIỆP THÀNH PHỐ HỒ CHÍ MINH Ths Ngô Quốc Nhàn BÀI GIẢNG TOÁN CAO CẤP A2 Hệ Đại Học Ngành: Thời lượng giảng dạy: 45 tiết TPHỒ CHÍ MINH-2016 LƯU HÀNH NỘI BỘ Mục lục 1 MA TRẬN- ĐỊNH THỨC 4 1
ĐẠI HỌC CÔNG NGHIỆP THÀNH PHỐ HỒ CHÍ MINH Ths Ngô Quốc Nhàn BÀI GIẢNG TOÁN CAO CẤP A2 Hệ Đại Học Ngành: Thời lượng giảng dạy: 45 tiết TPHỒ CHÍ MINH-2016 LƯU HÀNH NỘI BỘ Mục lục 1 MA TRẬN- ĐỊNH THỨC 4 1
2014 SPECIAL TNPSC Group II & VAO த ர வ க க பன பட ம க பக க ன ல ன -ல ட கள - 1 -
 04 SPECIAL TNPSC Group II & VAO த ர வ க க பன பட ம க பக க ன ல ன -ல ட கள - - JC - - JC - 3 - m - SI - 4 - MKS SI SI MKSA MKSA RAsionalised Metre Kilogram Second Ampere RMKSA SI SI (m) (Kg) (s) (A) (k) (cd)
04 SPECIAL TNPSC Group II & VAO த ர வ க க பன பட ம க பக க ன ல ன -ல ட கள - - JC - - JC - 3 - m - SI - 4 - MKS SI SI MKSA MKSA RAsionalised Metre Kilogram Second Ampere RMKSA SI SI (m) (Kg) (s) (A) (k) (cd)
inside 1
 Unkw_À 2018, ]pkvxiw 20, e w 12 kvt\l-ip-{iq-jm-ebw [ym\-ti{µw ku v NnäqÀ ]n. H., sim n 682 027 ticf, C y. NnäqÀ [ym\-ti{µ nsâ Hm^okv : Ph : 91 9446040508, 0484 2432508 Email : mail@chittoordyanakendram.com
Unkw_À 2018, ]pkvxiw 20, e w 12 kvt\l-ip-{iq-jm-ebw [ym\-ti{µw ku v NnäqÀ ]n. H., sim n 682 027 ticf, C y. NnäqÀ [ym\-ti{µ nsâ Hm^okv : Ph : 91 9446040508, 0484 2432508 Email : mail@chittoordyanakendram.com
TRƯỜNG ĐẠI HỌC HÙNG VƯƠNG DaNH SÁCH CÁC LỚP HỌC PHẦN (DỰ KIẾN) HỌC KỲ 2 - NĂM HỌC Trang 1 STT Tên lớp HP Tên học phần Mã HP Nhóm TC Mã Lớp XTKB
 TRƯỜNG ĐẠI HỌC HÙNG VƯƠNG DaNH SÁCH CÁC LỚP HỌC PHẦN (DỰ KIẾN) HỌC KỲ 2 - NĂM HỌC 16-17 Trang 1 1 AN1259 _01 Thực hành sư phạm âm nhạc AN1259 01 2 1412D60A 2 AN2206 _01 Lí thuyết âm nhạc cơ bản 2 AN2206
TRƯỜNG ĐẠI HỌC HÙNG VƯƠNG DaNH SÁCH CÁC LỚP HỌC PHẦN (DỰ KIẾN) HỌC KỲ 2 - NĂM HỌC 16-17 Trang 1 1 AN1259 _01 Thực hành sư phạm âm nhạc AN1259 01 2 1412D60A 2 AN2206 _01 Lí thuyết âm nhạc cơ bản 2 AN2206
!"# $%!&', 8 8 )*+, M "b#$ %_ ` ab5 G "K O6`?P[ G : 232c PAB 8 -CD5678 D 8 - PU V /4 I &'c -8 -I /4 8 -CD568 PQ7ab I W /4 8 -CD567 8-
 !"# $%!&', 88*+, M "b#$ %_ ` ab5 G "K O6`P[ G 22c +>4 @PB8 -CD5678D 8 -PU V 0-8 - 7 4 I&'c -8 -I 4 8 -CD568 PQ7ab I W 4 8 -CD567 8-8 -I 7 > W P + 2 4*5 18--8-7 - 4 V W 7 ' P Q - c X + c @ 4B 8-78I W2 9
!"# $%!&', 88*+, M "b#$ %_ ` ab5 G "K O6`P[ G 22c +>4 @PB8 -CD5678D 8 -PU V 0-8 - 7 4 I&'c -8 -I 4 8 -CD568 PQ7ab I W 4 8 -CD567 8-8 -I 7 > W P + 2 4*5 18--8-7 - 4 V W 7 ' P Q - c X + c @ 4B 8-78I W2 9
! " # $ %&' & ( ' 4 X O 3! `ab/ \] %7 )*+! G! bb %? %&V0"! 18 < 8 CV0Bc ' $ 1 8`aCV0] 2 8G ' $ 8D X Z ^ W 8 "3 D 9 VG 8 B C 8L ' Va;# T + 8= 4 8V0B. O
![! # $ %&' & ( ' 4 X O 3! `ab/ \] %7 )*+! G! bb %? %&V0! 18 < 8 CV0Bc ' $ 1 8`aCV0] 2 8G ' $ 8D X Z ^ W 8 3 D 9 VG 8 B C 8L ' Va;# T + 8= 4 8V0B. O ! # $ %&' & ( ' 4 X O 3! `ab/ \] %7 )*+! G! bb %? %&V0! 18 < 8 CV0Bc ' $ 1 8`aCV0] 2 8G ' $ 8D X Z ^ W 8 3 D 9 VG 8 B C 8L ' Va;# T + 8= 4 8V0B. O](/thumbs/100/145820547.jpg) !"#$ %&'& ('4X O 3! `ab/\]%7)*+! G! bb%? %&V0"!18
!"#$ %&'& ('4X O 3! `ab/\]%7)*+! G! bb%? %&V0"!18
TẬP ĐOÀN DỆT - MAY VIỆT NAM CỘNG HÒA XÃ HỘI CHỦ NGHĨA VIỆT NAM CTCP TỔNG CTY MAY ĐỒNG NAI Độc lập - Tự do - Hạnh phúc M 14 Số: 458/NQ - ĐHCĐ Đồng Nai,
 TẬP ĐOÀN DỆT - MAY VIỆT NAM CỘNG HÒA XÃ HỘI CHỦ NGHĨA VIỆT NAM CTCP TỔNG CTY MAY ĐỒNG NAI Độc lập - Tự do - Hạnh phúc M 14 Số: 458/NQ - ĐHCĐ Đồng Nai, ngày 30 tháng 3 năm 2013 NGHỊ QUYẾT Đại hội đồng cổ
TẬP ĐOÀN DỆT - MAY VIỆT NAM CỘNG HÒA XÃ HỘI CHỦ NGHĨA VIỆT NAM CTCP TỔNG CTY MAY ĐỒNG NAI Độc lập - Tự do - Hạnh phúc M 14 Số: 458/NQ - ĐHCĐ Đồng Nai, ngày 30 tháng 3 năm 2013 NGHỊ QUYẾT Đại hội đồng cổ
New Listings
 CBOE Research Circular #RS06-401 DATE: May 11, 2006 TO: Members RE: New Listings Abaxis, Inc. (ABAX) Abaxis, Inc. - 2008 Leap Aspreva Pharmaceuticals Corp. (ASPV) Active Date - 5/12/2006 Active Date -
CBOE Research Circular #RS06-401 DATE: May 11, 2006 TO: Members RE: New Listings Abaxis, Inc. (ABAX) Abaxis, Inc. - 2008 Leap Aspreva Pharmaceuticals Corp. (ASPV) Active Date - 5/12/2006 Active Date -
/ & : H ) NLZ 6 6& 4 L L L = < / L _ W M 9: 4 W! :(.6( O ( G Y / & <D23 : H,$0 6 #)A Q S / )C - Y H. L * R * T.).LV O 1 S* ).6( C M T. : ) G.6N ( * *U
 /& ) NL &4 L L L /L _M:4 (( O ( GY/&3,$#)A Q S/)C-Y L R T)LVO S ) ( C M T ) G N ( MM (( ) Y(G ( T GO8)7M )G ( ) T)8 # "#$ 3 %&'8+#&'#### %%%'4:&4( &&'& #%&'' "&'$&#" 3+ 4 +( %"' @@%' %%'- ' C%$''%+:$$'-$'%%'
/& ) NL &4 L L L /L _M:4 (( O ( GY/&3,$#)A Q S/)C-Y L R T)LVO S ) ( C M T ) G N ( MM (( ) Y(G ( T GO8)7M )G ( ) T)8 # "#$ 3 %&'8+#&'#### %%%'4:&4( &&'& #%&'' "&'$&#" 3+ 4 +( %"' @@%' %%'- ' C%$''%+:$$'-$'%%'
ỦY BAN NHÂN DÂN THÀNH PHỐ HÒ CHÍ MINH CỘNG HÒA XÃ HỘI CHỦ NGHĨA VIỆT NAM Độc lập - Tự do - Hạnh phúc Số: ylems? /QĐ-UBND Thành phổ Hồ Chí Minh, ngày i
 ỦY BAN NHÂN DÂN THÀNH PHỐ HÒ CHÍ MINH CỘNG HÒA XÃ HỘI CHỦ NGHĨA VIỆT NAM Độc lập - Tự do - Hạnh phúc Số: ylems? /QĐ-UBND Thành phổ Hồ Chí Minh, ngày id tháng 3 năm 2018 QUYẾT ĐỊNH về ban hành Kế hoạch
ỦY BAN NHÂN DÂN THÀNH PHỐ HÒ CHÍ MINH CỘNG HÒA XÃ HỘI CHỦ NGHĨA VIỆT NAM Độc lập - Tự do - Hạnh phúc Số: ylems? /QĐ-UBND Thành phổ Hồ Chí Minh, ngày id tháng 3 năm 2018 QUYẾT ĐỊNH về ban hành Kế hoạch
Bài 11: Phân tích dữ liệu mô phỏng Under construction.
 Bài 11: Phân tích dữ liệu mô phỏng Under construction. Sai số Sai số tính từ N phép đo độc lập hoặc thu được từ mô phỏng: N A = 1 N i=1 A i mean value σ= 1 N N 1 i=1 ( A i A ) 2 unbiased standard deviation
Bài 11: Phân tích dữ liệu mô phỏng Under construction. Sai số Sai số tính từ N phép đo độc lập hoặc thu được từ mô phỏng: N A = 1 N i=1 A i mean value σ= 1 N N 1 i=1 ( A i A ) 2 unbiased standard deviation
hªr f ecnñ-1 l Ù¹ l f n J AeÉeÉ MäS j a (pll l), he J h NQ pªs e Hhw gm i Nl A dl l fëc el B hce fœ (f ua LaÑ«L cçl L) fëll x
 hªr f ecnñ-1 l Ù¹ l f n J AeÉeÉ MäS j a (pll l), he J h NQ pªs e Hhw gm i Nl A dl l fëc el B hce fœ (f ua LaÑ«L cçl L) fëll x ----------------------------- ----------------------------- NË j f ua/ f ua
hªr f ecnñ-1 l Ù¹ l f n J AeÉeÉ MäS j a (pll l), he J h NQ pªs e Hhw gm i Nl A dl l fëc el B hce fœ (f ua LaÑ«L cçl L) fëll x ----------------------------- ----------------------------- NË j f ua/ f ua
BỘ GIÁO DỤC VÀ ĐÀO TẠO TRƯỜNG ĐẠI HỌC SƯ PHẠM HÀ NỘI 2 o0o NGUYỄN TRUNG DŨNG TÍNH ỔN ĐỊNH VÀ ỔN ĐỊNH HÓA CỦA MỘT SỐ LỚP HỆ NHẢY MARKOV RỜI RẠC LUẬN ÁN
 BỘ GIÁO DỤC VÀ ĐÀO TẠO TRƯỜNG ĐẠI HỌC SƯ PHẠM HÀ NỘI 2 o0o NGUYỄN TRUNG DŨNG TÍNH ỔN ĐỊNH VÀ ỔN ĐỊNH HÓA CỦA MỘT SỐ LỚP HỆ NHẢY MARKOV RỜI RẠC LUẬN ÁN TIẾN SĨ TOÁN HỌC HÀ NỘI, 2018 BỘ GIÁO DỤC VÀ ĐÀO TẠO
BỘ GIÁO DỤC VÀ ĐÀO TẠO TRƯỜNG ĐẠI HỌC SƯ PHẠM HÀ NỘI 2 o0o NGUYỄN TRUNG DŨNG TÍNH ỔN ĐỊNH VÀ ỔN ĐỊNH HÓA CỦA MỘT SỐ LỚP HỆ NHẢY MARKOV RỜI RẠC LUẬN ÁN TIẾN SĨ TOÁN HỌC HÀ NỘI, 2018 BỘ GIÁO DỤC VÀ ĐÀO TẠO
TRƯỜNG ĐẠI HỌC MỞ THÀNH PHỐ HỒ CHÍ MINH PHÒNG QUẢN LÝ ĐÀO TẠO CỘNG HÒA XÃ HỘI XÃ HỘI CHỦ NGHĨA VIỆT NAM Độc lập - Tự do - Hạnh phúc LỊCH THI HỌC KỲ 2
 TRƯỜNG ĐẠI HỌC MỞ THÀNH PHỐ HỒ CHÍ MINH PHÒNG QUẢN LÝ ĐÀO TẠO CỘNG HÒA XÃ HỘI XÃ HỘI CHỦ NGHĨA VIỆT NAM Độc lập - Tự do - Hạnh phúc LỊCH THI HỌC KỲ 2 NĂM HỌC 2016-2017 HỆ VĂN BẰNG 2 VÀ HOÀN CHỈNH KIẾN
TRƯỜNG ĐẠI HỌC MỞ THÀNH PHỐ HỒ CHÍ MINH PHÒNG QUẢN LÝ ĐÀO TẠO CỘNG HÒA XÃ HỘI XÃ HỘI CHỦ NGHĨA VIỆT NAM Độc lập - Tự do - Hạnh phúc LỊCH THI HỌC KỲ 2 NĂM HỌC 2016-2017 HỆ VĂN BẰNG 2 VÀ HOÀN CHỈNH KIẾN
Phó Đức Tài Giáo trình Đại số tuyến tính
 Phó Đức Tài Giáo trình Đại số tuyến tính 1 2 0 2 2 1 0 2 1 2 2 0 2 1 1 0 1 1 1 0 2 2 2 1 2 0 1 0 1 1 2 0 1 0 2 1 2 0 1 0 2 1 2 1 2 1 0 0 0 1 1 0 0 1 1 1 1 1 0 1 2 1 0 1 0 0 2 0 0 2 0 0 2 2 1 2 0 0 0 1
Phó Đức Tài Giáo trình Đại số tuyến tính 1 2 0 2 2 1 0 2 1 2 2 0 2 1 1 0 1 1 1 0 2 2 2 1 2 0 1 0 1 1 2 0 1 0 2 1 2 0 1 0 2 1 2 1 2 1 0 0 0 1 1 0 0 1 1 1 1 1 0 1 2 1 0 1 0 0 2 0 0 2 0 0 2 2 1 2 0 0 0 1
(LU HÀNH NI B) TÀI LIU ÔN TP HC K I Môn: Toán Khi: 11 Ban: T nhiên Giáo viên son: Nguyn Thanh D ng Eakar, tháng 12 nm 2010
 (LU HÀNH NI B) TÀI LIU ÔN TP HC K I Môn: Toán Khi: Ban: T nhiên Giáo viên son: Nguyn Thanh D ng Eakar, tháng nm 00 LI NÓI U Tài liu này giúp các em hc sinh lp (ban t nhiên) h thng li các kin th c c bn
(LU HÀNH NI B) TÀI LIU ÔN TP HC K I Môn: Toán Khi: Ban: T nhiên Giáo viên son: Nguyn Thanh D ng Eakar, tháng nm 00 LI NÓI U Tài liu này giúp các em hc sinh lp (ban t nhiên) h thng li các kin th c c bn
MỤC TIÊU VÀ CHUẨN ĐẦU RA CỦA CHƯƠNG TRÌNH ĐÀO TẠO
 464 CHƢƠNG TRÌNH ĐÀO TẠO ĐẠI HỌC Ngành học: Kỹ thuật vật liệu (Materials engineering) Mã ngành: 52520309 Hệ đào tạo: Chính quy Thời gian đào tạo: 4,5 năm Danh hiệu: Cử nhân Đơn vị quản lý: Bộ môn Công
464 CHƢƠNG TRÌNH ĐÀO TẠO ĐẠI HỌC Ngành học: Kỹ thuật vật liệu (Materials engineering) Mã ngành: 52520309 Hệ đào tạo: Chính quy Thời gian đào tạo: 4,5 năm Danh hiệu: Cử nhân Đơn vị quản lý: Bộ môn Công
Người ký: Ủy ban Nhân dân tỉnh Gia Lai vn Cơ quan: Tỉnh Gia Lai Thời gian ký: :46:52 +07:00 CONG HOA XA HOI C
 Người ký: Ủy bn Nhân dân tỉnh Gi Li Emil: ubndtinh@gili.gv. vn ơ qun: Tỉnh Gi Li Thời gin ký: 9.4.218 16:46:52 +7: NG HOA XA HOI HID NGHiA VitT NAM H lp - Tty d - Hunh phti UY BAN NHAN DAN TiNH GIA LAI
Người ký: Ủy bn Nhân dân tỉnh Gi Li Emil: ubndtinh@gili.gv. vn ơ qun: Tỉnh Gi Li Thời gin ký: 9.4.218 16:46:52 +7: NG HOA XA HOI HID NGHiA VitT NAM H lp - Tty d - Hunh phti UY BAN NHAN DAN TiNH GIA LAI
ĐẠI HỌC QUỐC GIA HÀ NỘI TRƯỜNG ĐẠI HỌC KHOA HỌC TỰ NHIÊN NGÔ THỊ THO PHƯƠNG PHÁP CHIẾU GIẢI BÀI TOÁN BẤT ĐẲNG THỨC BIẾN PHÂN GIẢ ĐƠN ĐIỆU MẠNH LUẬN VĂ
 ĐẠI HỌC QUỐC GIA HÀ NỘI TRƯỜNG ĐẠI HỌC KHOA HỌC TỰ NHIÊN NGÔ THỊ THO PHƯƠNG PHÁP CHIẾU GIẢI BÀI TOÁN BẤT ĐẲNG THỨC BIẾN PHÂN GIẢ ĐƠN ĐIỆU MẠNH LUẬN VĂN THẠC SĨ TOÁN HỌC Hà Nội - 205 ĐẠI HỌC QUỐC GIA HÀ
ĐẠI HỌC QUỐC GIA HÀ NỘI TRƯỜNG ĐẠI HỌC KHOA HỌC TỰ NHIÊN NGÔ THỊ THO PHƯƠNG PHÁP CHIẾU GIẢI BÀI TOÁN BẤT ĐẲNG THỨC BIẾN PHÂN GIẢ ĐƠN ĐIỆU MẠNH LUẬN VĂN THẠC SĨ TOÁN HỌC Hà Nội - 205 ĐẠI HỌC QUỐC GIA HÀ
BỘ GIÁO DỤC VÀ ĐÀO TẠO TRƯỜNG ĐẠI HỌC SƯ PHẠM TP. HỒ CHÍ MINH Nguyễn Minh Phong MỐI LIÊN HỆ GIỮA HÌNH HỌC TỔNG HỢP VÀ HÌNH HỌC GIẢI TÍCH TRONG DẠY HỌC
 BỘ GIÁO DỤC VÀ ĐÀO TẠO TRƯỜNG ĐẠI HỌC SƯ PHẠM TP. HỒ CHÍ MINH Nguyễn Minh Phong MỐI LIÊN HỆ GIỮA HÌNH HỌC TỔNG HỢP VÀ HÌNH HỌC GIẢI TÍCH TRONG DẠY HỌC HÌNH HỌC LỚP 12 Ở VIỆT NAM LUẬN VĂN THẠC SĨ GIÁO DỤC
BỘ GIÁO DỤC VÀ ĐÀO TẠO TRƯỜNG ĐẠI HỌC SƯ PHẠM TP. HỒ CHÍ MINH Nguyễn Minh Phong MỐI LIÊN HỆ GIỮA HÌNH HỌC TỔNG HỢP VÀ HÌNH HỌC GIẢI TÍCH TRONG DẠY HỌC HÌNH HỌC LỚP 12 Ở VIỆT NAM LUẬN VĂN THẠC SĨ GIÁO DỤC
TỊNH TIẾN VÀ ĐỐI XỨNG 1. Dựng đường thẳng có phương cho trước và bị hai đường tròn cho trước chắn thành hai dây cung bằng nhau. 2. Trên hai đường tròn
 TỊNH TIẾN VÀ ĐỐI XỨNG 1. Dựng đường thẳng có phương cho trước và bị hai đường tròn cho trước chắn thành hai dây cung bằng nhau. 2. Trên hai đường tròn bằng nhau (O) và (O ) lần lượt lấy hai cung AM và
TỊNH TIẾN VÀ ĐỐI XỨNG 1. Dựng đường thẳng có phương cho trước và bị hai đường tròn cho trước chắn thành hai dây cung bằng nhau. 2. Trên hai đường tròn bằng nhau (O) và (O ) lần lượt lấy hai cung AM và
q2-00-noidung
 Hình bià do hoạ sĩ TRẦN VĂN TUÔI ở San Jose (USA) trình bày (2003) Q2-noidung 1 02/01/05 QUYỂN HAI ĐOÁN MỆNH THEO TỪNG LÃNH VỰC VỚI CÁC THÍ DỤ ĐIỂN HÌNH Quyển 2 này tổng hợp tất cả những yếu tố cơ sở (như
Hình bià do hoạ sĩ TRẦN VĂN TUÔI ở San Jose (USA) trình bày (2003) Q2-noidung 1 02/01/05 QUYỂN HAI ĐOÁN MỆNH THEO TỪNG LÃNH VỰC VỚI CÁC THÍ DỤ ĐIỂN HÌNH Quyển 2 này tổng hợp tất cả những yếu tố cơ sở (như
Microsoft Word 四技二專-機械群專二試題
 第一部分 : 機械製造 1. Úd ØÇk g  Þg ¼ à º v «(A) º «(B) Þ «(C) ï «(D) «2. é Î Ýx ¹ kp é j ï uy ï } Žµ u Þ p Çv (A) ô ( Al2O 3) (B) (TiCN) (C) (TiN) (D) f(tac) 3. ÓŒ ± ¹ Ô ï p Ô Ç (A) (B) (C) (D) ïô 4. p ï h
第一部分 : 機械製造 1. Úd ØÇk g  Þg ¼ à º v «(A) º «(B) Þ «(C) ï «(D) «2. é Î Ýx ¹ kp é j ï uy ï } Žµ u Þ p Çv (A) ô ( Al2O 3) (B) (TiCN) (C) (TiN) (D) f(tac) 3. ÓŒ ± ¹ Ô ï p Ô Ç (A) (B) (C) (D) ïô 4. p ï h
687 ^dz c / ix j (s> /f~~v4 Cyy~iiÆ^ <_^ ia J j M-<f e tx - f( L. A^ ~ (VIUUI&L j 0 '" v 'V ^_A_jU-e^/> é í Cx^yicu^j^Ár U^X-Ciy^ <^"M_ jtjj Oi^L^Xo O
 687 dzc x j (> f~~v4 C~Æ _ j Mf e tx f( L. ~ (VUU&L j 0 '" v 'V jue> é í CxcjÁr UXC "M_ jtjj OLXo O v trw LCínrU í VÍjrtrtT' (4>fl V Le m \j L U Á C L C j > tjá H * djotltí C cx_ O* «X U T o í fd L t t
687 dzc x j (> f~~v4 C~Æ _ j Mf e tx f( L. ~ (VUU&L j 0 '" v 'V jue> é í CxcjÁr UXC "M_ jtjj OLXo O v trw LCínrU í VÍjrtrtT' (4>fl V Le m \j L U Á C L C j > tjá H * djotltí C cx_ O* «X U T o í fd L t t
THANH TÙNG BÀI TOÁN CHÌA KHÓA GIẢI HÌNH HỌC OXY Trong các năm gần đây đề thi Đại Học
 BÀI TOÁN CHÌA KHÓA GIẢI HÌNH HỌC OXY Trong các năm gần đây đề thi Đại Học môn toán luôn xuất hiện câu hỏi hình học Oxy và gây khó dễ cho không ít các thí sinh. Các bạn luôn gặp khó khăn trong khâu tiếp
BÀI TOÁN CHÌA KHÓA GIẢI HÌNH HỌC OXY Trong các năm gần đây đề thi Đại Học môn toán luôn xuất hiện câu hỏi hình học Oxy và gây khó dễ cho không ít các thí sinh. Các bạn luôn gặp khó khăn trong khâu tiếp
ĐẠI HỌC HUẾ TRƯỜNG ĐẠI HỌC SƯ PHẠM ĐẶNG HỮU ĐỊNH KHẢO SÁT CÁC TÍNH CHẤT PHI CỔ ĐIỂN VÀ VẬN DỤNG CÁC TRẠNG THÁI PHI CỔ ĐIỂN VÀO THÔNG TIN LƯỢNG TỬ LUẬN
 ĐẠI HỌC HUẾ TRƯỜNG ĐẠI HỌC SƯ PHẠM ĐẶNG HỮU ĐỊNH KHẢO SÁT CÁC TÍNH CHẤT PHI CỔ ĐIỂN VÀ VẬN DỤNG CÁC TRẠNG THÁI PHI CỔ ĐIỂN VÀO THÔNG TIN LƯỢNG TỬ LUẬN ÁN TIẾN SĨ VẬT LÝ HUẾ - NĂM 2017 i ĐẠI HỌC HUẾ TRƯỜNG
ĐẠI HỌC HUẾ TRƯỜNG ĐẠI HỌC SƯ PHẠM ĐẶNG HỮU ĐỊNH KHẢO SÁT CÁC TÍNH CHẤT PHI CỔ ĐIỂN VÀ VẬN DỤNG CÁC TRẠNG THÁI PHI CỔ ĐIỂN VÀO THÔNG TIN LƯỢNG TỬ LUẬN ÁN TIẾN SĨ VẬT LÝ HUẾ - NĂM 2017 i ĐẠI HỌC HUẾ TRƯỜNG
!"#$ %& ' '' ' ()*+,-./01 / :; 4 <= A ' F G HIJKL 50M NO %& ' PQRS TUVW X Y!"#$%&' $(' ) * +,-./ "* 9: -; < =>
 !"#$ %& ' ''' ()*+,-./01 / 23456-7 8-9 :; 4 ?@ A ' BC4
!"#$ %& ' ''' ()*+,-./01 / 23456-7 8-9 :; 4 ?@ A ' BC4
